前言
本系列是我在做人工智能高性能推理的工作中一些经验、思考和感悟,主要针对的范畴是深度神经网络的高性能推理,多以 CPU Arm 环境为例,但在 x86、 GPU 环境下一般也同样适用。
概念
给定以下系统,阿姆达尔定律给出了性能优化究竟能带来多少提升。
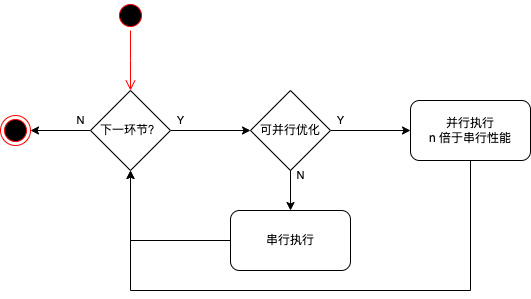
所描述的系统是这样的:
1. 任务是一环扣一环,每个环节依次顺序执行
2. 在每个环节内部,都可能是串行或者并行执行。如果是串行,那么性能归一化为 1;如果是并行,那么性能是串行的 n 倍,n 是多少取决于并行化的程度
3. 性能优化只包含以下 3 种:
1. 要么增减环节的数量
2. 要么将某个环节从串行变为并行(或者相反)
3. 要么调整某个环节的并行的 n
4. 也就是说,将整个任务重构为新的一些环节,打散并融合一些环节内部的流程,从而形成一个新的系统。这样的做法不在讨论的范围之中,因为重构后的系统的串行的归一化性能 “1” 与旧系统不再具有可比性。
具体而言,阿姆达尔定律(Amdahl’s Law)如下:
AM = 1 / ( (1-prl) + prl/n )
– prl (parellel) 是并行化程度(百分比),指有百分之多少的环节是并行化的
– n 是并行化倍数
例如,假设系统只有一个环节,该环节为:
– 串行,则 prl = 0,AM = 1
– 并行,则 prl = 1,AM = n
细心的读者会发现上面的描述似乎存在一个漏洞:性能优化可以调整某个环节的并行的 n,而公式中又只包含了一个 n,是不是意味着定律约定了所有环节的并行化提升都必须共享了同一个 n 值?
实际上不必如此考虑,每个环节都可以有自己独立的并行化 n 倍提升。我们只需要对同一个系统递归地应用同样的方法,每一个递归步都只针对一个环节进行分析,就可以做到既只使用一个 n 值,又能分析到每个环节。
从宏观上理解
假设一个任务有一环可以并行化加速,但是这个任务有若干环节。我们是应该优先优化流程、减少环节,还是尽力将并行化这一环做到极致呢?
阿姆达尔定律恰好可以给于我们很好的指导。我们来做一个测算。
为了测算能在具体数字上展开,当然需要做一些预设,这些预设只影响测算的数字,但不影响整个分析方法的思路。预设如下:
– 任务可以有 1、2、… 10 等多个环节,每个环节的耗时都一样
– 只有一个环节能做并行优化,因此 prl 对应是 100%, 50%, 33%, 25%,…… 10%
– 并行优化的程度(n),最多可以到 1000 倍
我们从 10 个环节、无并行优化(n=1)开始,优化手段只有减少环节,或者提高并行度两种。使用 Excel 就可以完成这样简单的测算:
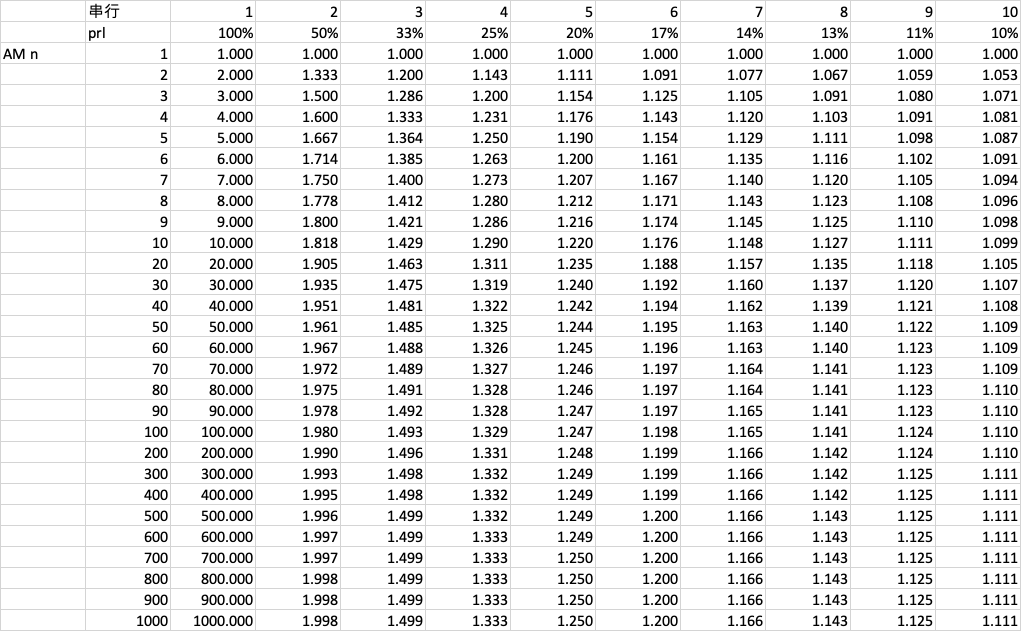
这样阅读测算结果即可:比较某一格的下方和左方。如果下 > 左,说明优化并行带来的提升更大;如果左 > 下,说明优化流程、减少环节带来的提升更大。注意纵坐标 n 大约是按 log10 来排列的。
测算结论:
– 并行 2 倍总是有收益
– 并行 4 倍之后,并行不再有收益,几乎都是优化减少一个串行环节的收益更高
这样的测算能给我们一个对性能优化带来多少收益的直观感受,但还是离实际问题有一定距离,切勿生搬硬套。在这个结果之上,至少需要再考虑减少环节,抑或是提高并行度,需要的 effort(花费多少“工夫”、克服多少困难),横纵数字对 effort 的归一化之后,才相对可比。
从微观上理解
具体到程序里,所谓高性能计算就是,给定某输入,我们需要尽可能高效地计算某输出。
(仅 CPU 的情况下)每一条非 SIMD 指令,都是任务的一个串行环节,直到我们遇到了如下结构,即一个嵌套的循环体,内部是一段几乎全是 SIMD 的高效计算的片段,此片段我们一般称为 micro-kernel。
因此整段代码的性能,是所有串行指令的 cycle + 循环数 * micro-kernel 的性能 约= 循环数 * micro-kernel 的性能 (因为串行 cycle 往往微乎其微,且更重要的是有限的)
micro-kernel 的性能应该这样评估:
总数据量 / 循环数 = micro-kernel 的数据量
在这个数据量下,共需要多少的 SIMD cycle 以及 cache-miss
因此,在高性能推理的开发过程中,一次优化过程总是这样的:对于同一个计算任务,即一样的数据量、一样的计算量,存在两种实现,它们分别有不同的循环数和 micro-kernel。通过分析两种实现的优劣,我们便得出了哪个更好的结论,最终完成一次性能提升的开发。
网络等公开资料上有很多高性能开发的指导,它们要么提到每条 SIMD 的吞吐和延迟,要么提到 micro-kernel 的 cache-miss 优化,都非常重要且切题,但我总嫌零碎,总觉得缺少点什么。因此,我认为首先这样考虑是有益的:从整体上把握一次完整的计算任务,把循环展开,一个接一个的 micro-kernel 的环节实际上符合一个完整的阿姆达尔定律的分析,每个 micro-kernel 内部也符合一个完整的分析。因此虽然有些 micro-kernel 的 cycle 数等是很低的,但是由于循环方式、访存 pattern 的不同,它们未必比得过其他一些看似复杂但实际上计算模式高效的方式。
PS:前文提到任务并行化 4 倍是相对最优的提升。从微观上看,Arm SIMD lane 刚好也是 4(当前 2024 的主流手机),而在 CPU superscalar 流水线中的每一步,又恰好有着相近的耗时,也算是一个有趣的巧合。不过实际的芯片设计可比一个 excel 表格要复杂得多了(废话……),芯片面积、功耗、工业价格、供应商价格、向前兼容的指令集等等,每一项都把问题的复杂度提高了一个数量级。